As a developer, it's important to understand the fundamental concepts of algorithmic thinking. But what are algorithms?

a set of mathematical instructions or rules that, especially if given to a computer, will help to calculate an answer to a problem - [1]

Algorithms are a set of instructions that help solve complex problems, and they are essential for creating efficient and scalable software. In this guide, we'll explore the basics of algorithmic thinking, including data structures, problem-solving techniques, and algorithm complexity.

We'll also look at common algorithm examples, tips for mastering algorithmic thinking, and resources for learning algorithms. Finally, we'll discuss how algorithmic thinking is used in software development and why it's important for developers to have a strong understanding of algorithms.

Understanding algorithms

Algorithms are used in many different fields, including computer science, where they are essential for creating efficient and scalable software. For example, algorithms can be used to sort large amounts of data, find the shortest path between two points, or solve complex mathematical problems.

Algorithms are specially important for software development because they enable software to perform complex tasks quickly and accurately. Without algorithms, these tasks would be time consuming and error prone. Therefore, having a strong understanding of algorithms is crucial for developers who want to create efficient and scalable web applications. In the following sections, we'll explore the basics of algorithmic thinking and why it's important for developers and to become a good developer to have a strong understanding of algorithms.

Making a sandwich

When making a sandwich, you follow a set of instructions in a specific order. For example, you might

1. start by taking two slices of bread,
2. add a filling (such as meat and cheese),
3. and then cut the sandwich in half.

This is a simple algorithm that you might not even realize you're following!

Brushing your teeth

When brushing your teeth, you follow a set of instructions in a specific order. For example, you might

1. wet your toothbrush,
2. add toothpaste,
3. brush your teeth in a circular motion,
4. and then rinse your mouth and toothbrush.

This is another simple algorithm that you might not think about consciously.

Vacuuming the floor (more complex algorithm)

There are times when you actually follow a set of more complex algorithm steps. When Vacuuming for example, you might

1. start by moving furniture out of the way,
2. then turning on the vacuum cleaner
3. and adjusting the settings for the type of flooring you're cleaning.
4. You might then work your way around the room in a specific pattern,
5. such as starting at the furthest corner and working your way back toward the door.
6. You might also use specific techniques, such as overlapping strokes or making sure to get into corners and under furniture.
7. Finally, you'll need to empty the vacuum cleaner and put everything back in its place.

But what “if”?

When driving to work, you might follow a set of instructions that depend on specific conditions. For example,

1. if there is heavy traffic on your usual route,

   1. you might decide to take an alternative route.

2. If you're running late,

   1. you might need to speed up or take a shortcut.

3. If it's raining or snowing,

   1. you might need to adjust your driving technique to ensure safety.

In each case, you are making a decision based on a specific condition or set of conditions, which is an example of an "if" statement that is commonly used while programming.

The whole point is, our brains are wired to analyze and solve problems using algorithms, even if we're not consciously aware of it. From the moment we wake up and start our daily routines, we're using algorithms to make decisions and perform tasks efficiently, as mentioned in the above examples, without even realizing that we're using an algorithm.

When it comes to learning programming, it's not necessary to imagine algorithms in your mind in order to understand them. Instead, you can focus on learning the fundamental concepts and techniques of algorithmic thinking, such as data structures, problem-solving techniques, and algorithm complexity. By mastering these concepts, you'll be able to apply them to a wide range of programming problems, whether you're working on web applications, software development, or any other field that requires algorithmic thinking.

Data structures and algorithms

Data structures and algorithms are fundamental concepts in computer science. A data structure is a way of organizing and storing data in a specific format, such as a list or a tree. An algorithm is a set of instructions for solving a problem, which can be applied to data structures to perform specific operations, such as searching, sorting, or inserting data.

A data structure?!

Let us examine some examples of data structures:

1. Grocery list: A grocery list is a data structure that organizes and stores a list of items you need to buy at the grocery store. Each item can be stored in a specific format, such as a bullet point or a numbered list, and can include additional information, such as the quantity or brand of the item.
2. Recipe book: A recipe book is a data structure that organizes and stores a list of recipes. Each recipe can be stored in a specific format, such as a step-by-step list or a paragraph of instructions, and can include additional information, such as the ingredients, cooking time, or serving size.
3. Address book: An address book is a data structure that organizes and stores a list of contacts. Each contact can be stored in a specific format, such as a name and phone number, and can include additional information, such as an address or email address.

Now I’m gonna stick to the last example, let’s see how it can be examined.

An address book

An address book is a data structure that stores a list of contacts, typically in alphabetical order. Each contact in the address book has a unique identifier, such as a name or a phone number, which can be used to quickly find and retrieve the contact's information.

In addition to the unique identifier, each contact can have multiple fields or attributes, such as an address, email address, or additional notes. These fields can be organized in a specific format, such as a table or a form, which makes it easy to view and update the information for each contact.

The address book can also include additional features, such as a search function (assuming it exists in a mobile phone) or the ability to sort contacts by different criteria, such as last name or ZIP code. These features make it easy to find and manage specific contacts and can be implemented using specific algorithms and data structures, such as search algorithms or sorting algorithms.

Categorization of data structures

There are many different types of data structures and algorithms, each with its own strengths and weaknesses. For example, a linked list is a data structure that can be used to store and manipulate a list of elements in a specific order. A search algorithm can be applied to a linked list to find a specific element or a sort algorithm can be used to organize the elements in a specific order.

Linear data structure

It's a way of organizing data where each item is connected to the one before and after it, in a straight line.

Static data structure

This type has a set size that doesn't change, hence static. Think of it like a box with a certain number of slots; you can't add more slots once it's made. This makes it straightforward to reach any item.

Dynamic data structure

Unlike static ones, these can change size as needed, hence dynamic. Imagine a bag where you can keep adding or removing things; it adjusts according to what's inside. This flexibility can be more memory-efficient

Non-Linear data structure

Unlike a straight line where each item follows the other, in non-linear structures, data is spread out in multiple directions. This means you can't go through all the items in just one straight path.

There are fundamental data structures existing in the computer engineering world, such as:

1. Arrays (Static linear data structure): An array can be used to store a collection of items of the same type, such as a list of names or a set of numerical values. For example, an array can be used to store the temperatures for each day of the week or the list of ingredients for a recipe.

   

   .

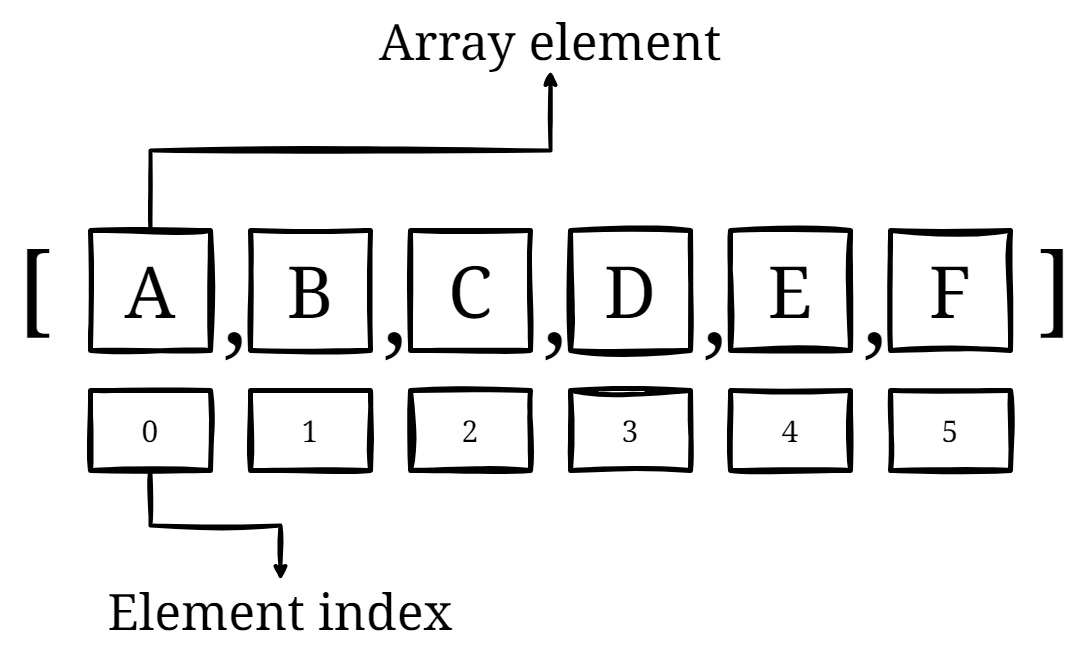
2. Linked lists (Dynamic linear data structure): A linked list can be used to store and manage a collection of items that need to be added or removed frequently, such as a playlist of songs or a queue of tasks. Each node in the linked list contains a data element and a pointer (just forget about it for now) to the next node in the list.

   

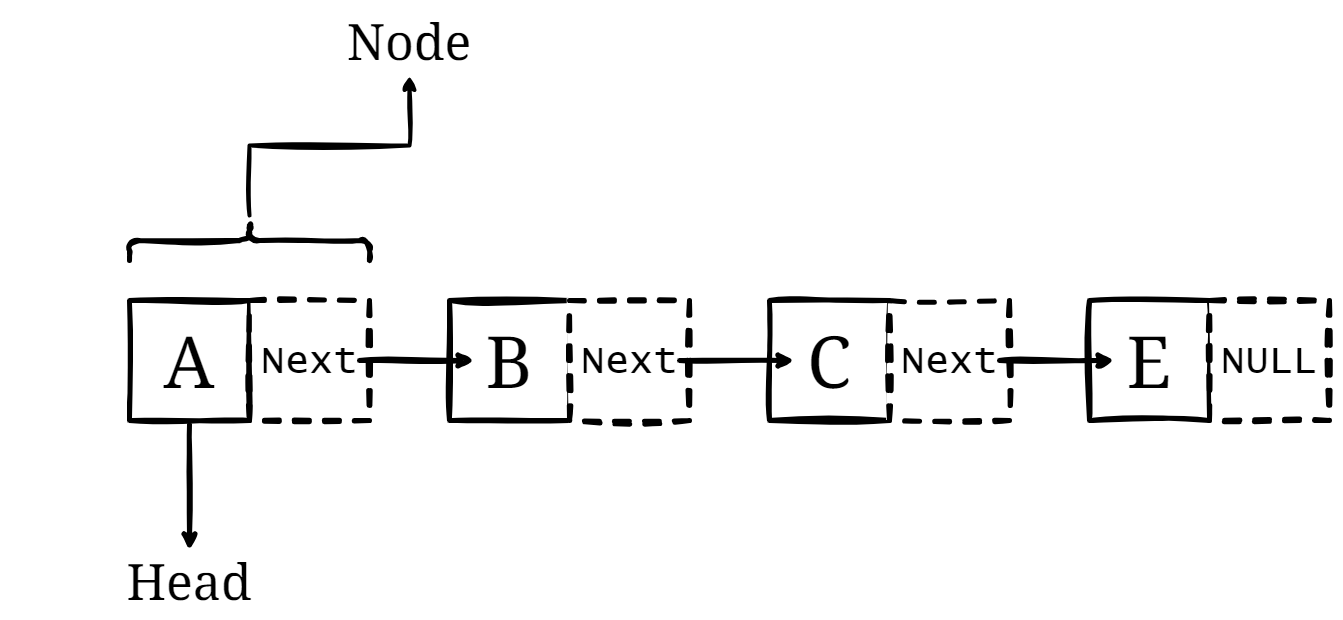
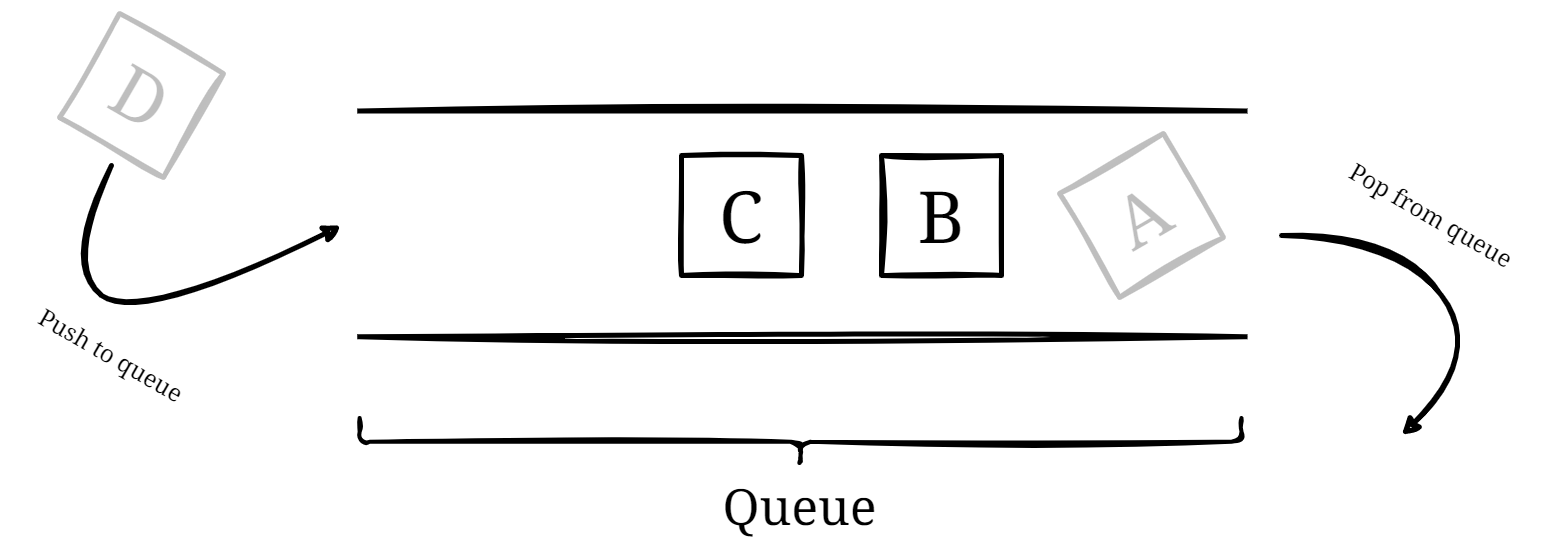
3. Stacks (Dynamic linear data structure): A stack can be used to implement an undo/redo function in a text editor or to manage a history of pages visited in a web browser. When an action is performed, it is added to the top of the stack, and when the user wants to undo or redo an action, the top element is removed from the stack and executed in reverse order, a so called “Last in, First out”.

   

4. Queues (Dynamic linear data structure): A queue can be used to manage a waiting list for a restaurant or a queue of customers waiting to buy tickets. Each time a customer joins the queue, they are added to the end of the line, and when it's their turn, they are removed from the front of the queue, exactly contrary to stacks, a so called “First in, First out”

   

5. Trees (Non-Linear data structure): A tree can be used to represent a family tree or a company organizational chart. Each node in the tree represents a person or a position, and the edges represent relationships or hierarchies between them.

   

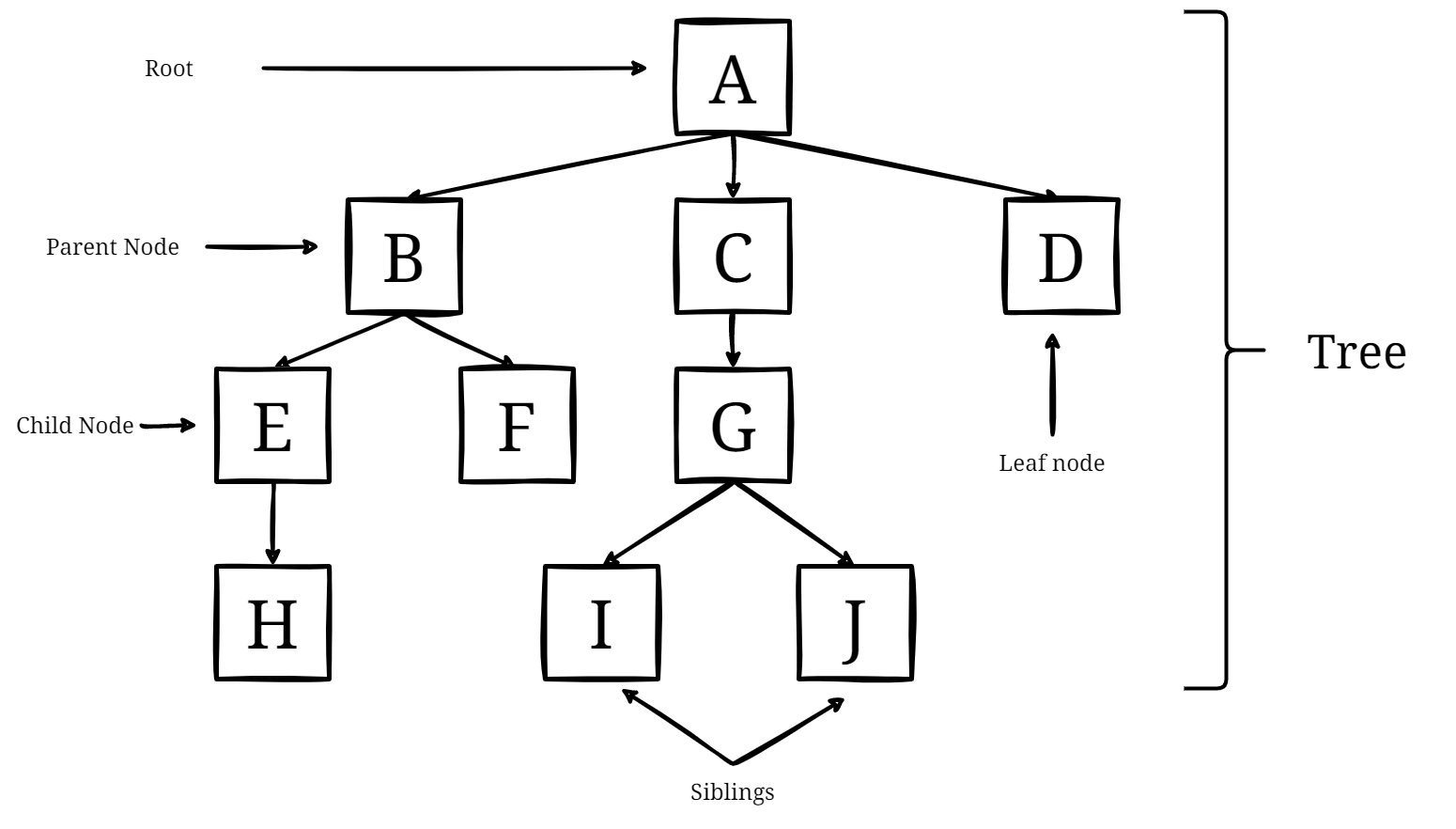
6. Graphs: A graph can be used to model social networks or transportation networks. Each node represents a person or a location, and the edges represent relationships or connections between them.

   

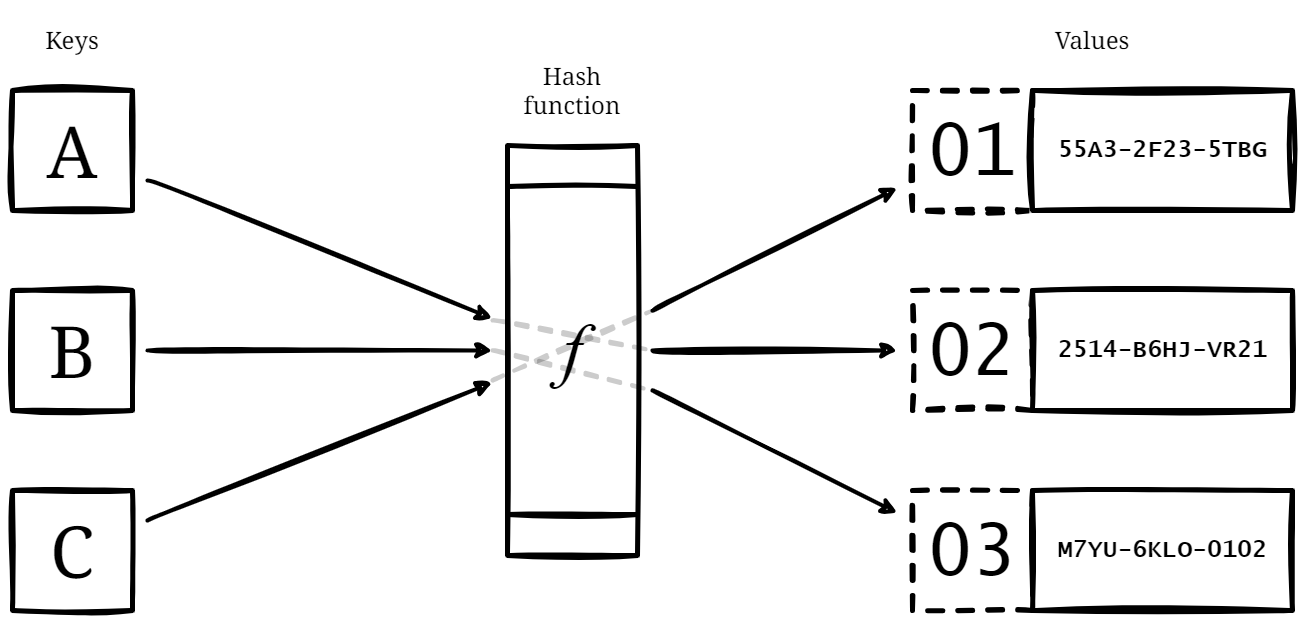
7. Hash tables: A hash table can be used to store and manage a collection of key-value pairs, such as a dictionary or a phone book. The keys are hashed to produce an index into a table, and the associated values can be quickly retrieved using the index.

   

8. Heaps: A heap can be used to implement a priority queue, where elements are removed in order of priority. For example, a heap can be used to manage the order in which emergency calls are processed or to schedule tasks based on their priority.

Choosing the right data structure and algorithm for a particular task is essential for creating efficient and scalable software. By understanding the strengths and weaknesses of different data structures and algorithms, you can choose the most appropriate ones for your specific needs and optimize your code for performance and scalability. In the next sections, we'll explore some common data structures and algorithms in more detail and discuss how they are used in software development.

Algorithmic problem-solving

Algorithmic problem-solving is a key skill for programmers and involves using algorithms to solve complex problems efficiently and effectively. One common approach to algorithmic problem-solving is the "divide and conquer" approach. This involves breaking a complex problem down into smaller, more manageable sub-problems, and then solving each sub-problem individually. This approach is particularly useful for problems that can be divided into independent sub-problems that can be solved concurrently.

Another important technique for algorithmic problem-solving is dynamic programming. This involves breaking a problem down into smaller sub-problems and then using the solutions to those sub-problems to solve the larger problem. This technique is particularly useful for problems that exhibit overlapping sub-problems, where the same sub-problem needs to be solved multiple times.

In addition to these techniques, there are many other algorithmic problem-solving strategies, such as brute force, backtracking, and greedy algorithms. Each strategy has its own strengths and weaknesses and can be applied to different types of problems. By understanding the principles of algorithmic problem-solving and mastering these techniques, you can become a more efficient and effective programmer and solve complex problems with ease.

Algorithmic problem-solving as life hacks

Now let’s explore the “way of algorithmic thinking” to boost your day-to-day life a bit. Of course, if you aren’t already using the following.

1. Making a to-do list: When faced with a large number of tasks, it can be overwhelming and difficult to know where to start. Using a divide-and-conquer approach, you can break your to-do list down into smaller, more manageable sub-tasks. This makes it easier to prioritize and tackle each task individually, leading to a more efficient and productive workflow.
2. Packing for a trip: When packing for a trip, it can be challenging to fit everything you need into a limited amount of space. Using dynamic programming, you can break down the problem of packing into smaller sub-problems, such as packing clothes, toiletries, and electronics. By optimizing each sub-problem individually, you can pack efficiently and avoid overpacking.
3. Organizing your wardrobe: When organizing your wardrobe, it can be challenging to keep track of all your clothes and accessories. Using a data structure such as an array or linked list, you can categorize and organize your clothes by type, color, or season. This makes it easier to find and select outfits, saving you time and reducing stress.
4. Budgeting and saving: When trying to save money, it can be challenging to stick to a budget and avoid overspending. Using greedy algorithms, you can optimize your spending and savings strategies to meet your financial goals. For example, you could use a divide-and-conquer approach to break down your budget into smaller categories, such as rent, utilities, and groceries, and then allocate funds accordingly.

These examples demonstrate how algorithmic problem-solving techniques can be applied to everyday scenarios, helping you to optimize your workflow, save time, and reduce stress. By using these techniques, you can become a more efficient problem-solver in all areas of your life.

Our very own pseudocode

Pseudocode is a simple, high-level “programming” language used to express algorithms. It's not meant to be executed but rather serves as a way to describe and plan out the steps of a program or algorithm. Pseudocode is often used in the early stages of development to help programmers think through their logic and plan out their code. Hence the usage here is to gain a better understanding of algorithms.

CW Language

This language is designed to help you understand and explain algorithms in an easy-to-understand way. Our language supports variables, data types, and statements, making it a great tool for describing complex algorithms.

Here are the keywords supported by our language:

• next: Jumps to the next iteration of a loop.
• do: Marks the beginning of a loop or conditional block.
• else: Marks the beginning of an alternative branch in a conditional block.
• for every: Iterates each element in an array or collection.
• jump to line <n>: Jumps to a specific line number in the code.
• if: Begins a conditional block that executes if a condition is true.
• else if: Begins an alternative conditional block that executes if the previous condition is false and the current condition is true.
• return: Exits a function and returns a value.
• set <something> to <another thing>: Sets the <something> to be equal (or better said: assigned) to <another thing>.
• length(<arr>): Returns the number of elements in an array <arr> or collection.
• until <condition> do: Executes a loop until the specified condition is true.

BubbleSort wrote in CW

Now, here's an example of how to use our pseudocode language to implement the bubble sort algorithm:

bubbleSort(arr):
  set n to length(arr)
  set swapped to true
  while swapped is true:
    set swapped to false
    for every i until i is n - 1 do:
      if arr[i] > arr[i+1]:
        set temp to arr[i]
        set arr[i] to arr[i+1]
        set arr[i+1] to temp
        set swapped to true
      next
    jump to line 4
  print arr

But what’s happening here?!

We begin by defining a function called bubbleSort that takes a list called arr  (arr as to be used for arrays, but right now we don’t want to jump into data types) as an argument.

In CW, functions are defined like this: functionName (parameters and arguments separated by comma):

For example the sinus function in math can be written like this:
sin(x):

We then set a variable n to the length of the array using the length(arr) keyword, or a bit more developer friendly said: we assign the value of length(arr) to the variable n. We also set a Boolean variable swapped to true to indicate that the array is not yet sorted. In this case, swapped is called a flag.

In CW, variables (such as the famous x in math) are created like this: set <variableName> to <the value you want to assign to it>

For example, x = 10 in math can be written as: set x to 10

We then enter a while loop that continues as long as swapped is true. Inside the loop, we set swapped to false to indicate that we have not yet swapped any elements.

while is a Loop in CW. A loop is a construct that allows a block of code to be executed repeatedly, either a fixed number of times or until a certain condition is met.

We then enter a for every loop that iterates over each element i in the array, up to the second-to-last element.

for is also a loop. In a for loop, which is written as for every in CW, a block of code is executed for a fixed number of times (in our scenario n-1 times). The loop initializes a counter variable (i) that ALWAYS starts from 0, checks a condition (until i = n-1), and increments the counter variable after each iteration until the condition is met.

Inside the loop, we check if the current element arr[i] (the (i+1)-th item in arr) is greater than the next element arr[i+1] (the i+2-th item in arr). If it is, we swap the elements by setting a temporary variable temp to arr[i], and then setting arr[i] to arr[i+1] and arr[i+1] to temp. We also set swapped to true to indicate that we have swapped elements.

At the end of the loop, if we have not swapped any elements, it means the array is sorted, and we can exit the loop. If we have swapped elements, we use the jump to line 4 keyword to jump back to the beginning of the loop to repeat the process.

Finally, we use the print keyword to print the sorted array.

Training

Try to fill out the following table. The idea is that we want to test the algorithm (bubble sort) for a list of numbers [5, 3, 8, 2, 1].

Iteration	Array		i	arr[i]	arr[i+1]	temp	swapped
1		[5, 3, 8, 2, 1]	0	5	3		5	True
2		[3, 5, 8, 2, 1]	1	5	8		-	False
3		[3, 5, 8, 2, 1]	2	8	2		8	True
4		[3, 5, 8, 2, 1]	3	2	1		...	...
5		...		...	...	...		...	...
6		...		...	...	...		...	...
7		...		...	...	...		...	...
8		...		...	...	...		...	...
9		...		...	...	...		...	...

Common algorithm examples

Algorithms are used to solve complex problems across many different fields, including computer science. There are many different types of algorithms, but some of the most common include sorting algorithms, searching algorithms, and graph algorithms.

Sorting algorithms are used to put a list of elements into a specific order, such as alphabetical or numerical. Common sorting algorithms include bubble sort, insertion sort, and quicksort. These algorithms work by repeatedly comparing and swapping elements in the list until they are in the correct order.

Searching algorithms are used to find a specific element within a dataset. Common searching algorithms include linear search and binary search. Linear search checks each element in the dataset one by one until it finds the desired element, while binary search is more efficient and works by repeatedly dividing the dataset in half until the desired element is found.

Graph algorithms are used to solve problems related to graphs, such as finding the shortest path between two points or determining if a graph is connected. Common graph algorithms include Dijkstra's algorithm and breadth-first search. These algorithms work by traversing the graph, either by visiting neighboring nodes or by maintaining a priority queue of nodes to visit next.

Understanding these common algorithm examples is critical for developing efficient and scalable software. By choosing the right algorithm for a given task, developers can optimize performance and reduce the time and resources required to complete the task.

Algorithm complexity

Algorithm complexity is an essential concept in computer science and refers to the efficiency of an algorithm. Two main factors determine algorithm complexity: time complexity and space complexity.

Time complexity refers to the amount of time an algorithm takes to complete a task, and it's typically measured in "Big O" notation. Big O notation describes how the time required by the algorithm grows as the size of the input data increases. An algorithm with a better time complexity will be faster and more efficient, particularly when dealing with large datasets.

Space complexity, on the other hand, refers to the amount of memory an algorithm requires to complete a task, and it's also typically measured in "Big O" notation. This is important because some algorithms can be very efficient in terms of time complexity, but may require a lot of memory to operate. It's essential to balance time and space complexity when designing algorithms to ensure they are efficient and scalable.

Understanding algorithm complexity is critical for optimizing code and improving performance. By analyzing the time and space complexity of an algorithm, you can identify potential bottlenecks and areas for optimization, leading to faster, more efficient code.

The Big O

I’ll first explain it in a technical and mathematical way that is more relevant to someone with a CS degree. Don’t worry, I’ll also bring easier examples just right after.

Now the Big O notation is a mathematical notation used to describe the upper bound of the time or space complexity of an algorithm. It's a way to analyze the efficiency of an algorithm by describing how its time or space requirements grow with the size of the input data.

In Big O notation, the upper bound of the growth rate is described in terms of a function, typically represented using the "O" symbol. For example, if an algorithm's time complexity grows linearly with the size of the input data, we can say that its time complexity is:

where n represents the size of the input. Now, if an algorithm's time complexity grows (frankly meaning that it takes more time to complete the algorithm) quadratically with the size of the input data, we can say that its time complexity is:

Big O notation is essential for analyzing the efficiency of algorithms and for choosing the most efficient algorithm for a given task. By understanding Big O notation, developers can optimize their code, reduce execution time, and minimize resource usage.

Talk less math!

Assume you are searching for an item in a grocery store. Suppose you're looking for a specific item in this large grocery store. If you search every aisle one by one until you find the item, your time complexity is O(n), where n is the number of aisles in the store. However, if you ask a store employee for help and they can quickly direct you to the item, your time complexity is O(1), eventually meaning the time required does not depend on the size of the store.

Now suppose you need to cook a meal for a large group of people. If you prepare each dish individually, the time required will be proportional to the number of dishes you need to prepare, resulting in a time complexity of O(n), where n is the number of dishes. However, if you use a slow cooker or pressure cooker, you can prepare multiple dishes simultaneously, reducing the time required and resulting in lower time complexity.

Make it a bit more complex

Assuming you need to find a particular book on a shelf that contains n books. Here are some scenarios that illustrate the different Big O notations:

O(n)

Suppose the books on the shelf are not organized in any particular order, and you need to search through each book one by one until you find the one you're looking for. The (worst) time required to find the book is proportional to the number of books on the shelf, resulting in a time complexity of O(n).

O(1)

Suppose the books on the shelf are organized in alphabetical order, and you know the exact title of the book you're looking for. You can immediately go to the location of the book, without having to search through any other books. The time required to find the book is constant, regardless of the number of books on the shelf, resulting in a time complexity of O(1).

O(n²)

Suppose you need to sort a pile of n papers, and you choose to do so by comparing each paper to every other paper to determine its correct order. This is a very inefficient way to sort, and it will take a time proportional to the square of the number of papers to complete the task, resulting in a time complexity of O(n²).

Training

Let us examine our BubbleSort algorithms Big O:

bubbleSort(arr):
  set n to length(arr)			// O(1)
  set swapped to true			// O(1)
  while swapped is true:		// O(n)
    set swapped to false		// O(1) x O(n) = O(n)
    for every i until n - 1 do:		// O(n) x O(n) = O(n^2) <- biggest O
      if arr[i] > arr[i+1]:
        set temp to arr[i]
        set arr[i] to arr[i+1]
        set arr[i+1] to temp
        set swapped to true
      next
    jump to line 4			// O(1) x O(n)
  print arr				// O(1)

The while loop in the algorithm executes n times in the worst case, where n is the number of elements in the input array. Within each iteration of the while loop, the for every loop also executes n times in the worst case, resulting in a total of n² iterations O(n²) in total.

Likelihood of errors when facing complex algorithms

The relationship between the complexity of an algorithm and the probability of errors is nuanced. So Let's break down the following important questions:

• Is the probability of errors proportional to the complexity of an algorithm?
• Are human more prone to errors when faced complex algos?
• And are there any studies in that regards?

Probability of Errors and Algorithmic Complexity

When an algorithm is complicated, it's often tougher to write it down without making mistakes, so coding errors can pop up more frequently. Similarly, the harder it is to wrap your head around an algorithm, the more likely you might get things wrong when you're trying to use or tweak it; this is what is called conceptual errors.

Then there's the challenge of spotting these mistakes. With these tricky algorithms, there can be many special scenarios and cases to consider and they might need a lot of testing, so spotting where things go wrong becomes a bigger task. And let's not forget the foundation of some algorithms: complicated math. If there's a mistake in that math, or if it's not turned into code just right, the whole algorithm can be off track.

Why We Make Mistakes with Tricky Algorithms

When we're faced with complicated algorithms, it's like juggling many thoughts at once. This can be overwhelming and can make us overlook things or mess up.

Often, we trust our gut feelings when dealing with tough problems. But sometimes, our gut can trick us, especially if the algorithm has some surprising twists. And, just like how we get tired after a long day, working on a tough problem for a long time can wear us out. When we're worn out, we're more likely to slip up. This will eventually cause Fatigue which by itself will cause more errors.

Studies

Cognitive science and human factors research have examined how humans handle complex tasks. A key concept here is "cognitive load," which refers to the mental effort required to process information and perform tasks. When cognitive load is high — as it might be when grappling with a complex algorithm — errors become more likely. [2]

In software engineering, on the other hand, experience on code readability, maintainability, and defect rates have shown that more complex code tends to have higher defect rates. This supports the notion that complexity might be linked to error rates.

Tips for mastering algorithmic thinking

Mastering algorithmic thinking takes time and practice, but there are several tips that can help you improve your problem-solving skills. One of the most important tips is to practice regularly. The more you practice, the more comfortable you will become with algorithms and data structures.

Another important tip is to study other people's code. Reading and understanding code written by others can help you learn new techniques and approaches to problem-solving.

Finally, it's important to be patient and persistent. Algorithmic thinking can be challenging, but with practice and persistence, you can become an expert at solving complex problems.

Algorithm resources

There are many resources available for learning algorithms, including books, courses, and online resources. Some of the best resources include:

• "Introduction to Algorithms" by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein
• "Algorithms, Part I" and "Algorithms, Part II" on Coursera by Robert Sedgewick and Kevin Wayne
• "Algorithm Design Manual" by Steven S. Skiena
• HackerRank and LeetCode, two popular online platforms for practicing algorithmic problem-solving.

Algorithmic thinking in software development

Algorithmic thinking is essential for developers. Algorithms are used to solve complex problems and make web applications more efficient and scalable.

Some common examples of algorithmic thinking in web development include optimizing database queries, caching frequently accessed data, and designing efficient algorithms for processing user input.

Having a strong understanding of algorithms and data structures can also help you choose the right tools and technologies for a project, and can make it easier to collaborate with other developers.

Conclusion

In conclusion, algorithmic thinking is an essential skill for developers. Understanding algorithms, data structures, and algorithmic problem-solving are key to creating efficient and scalable web applications. By following the tips and resources outlined in this guide, you can improve your algorithmic thinking skills and become a more effective web developer.

1. “algorithm.” Aug. 09, 2023. Available: https://dictionary.cambridge.org/dictionary/english/algorithm
2. M. Doorey, “George A. Miller | American Psychologist & Cognitive Scientist,” Encyclopedia Britannica, Jul. 18, 2023. Available: https://www.britannica.com/biography/George-A-Miller#ref1200615